Cours n°4 - Arc en ciel

L'arc en ciel résulte d'une réflexion des rayons solaires à l’intérieur de gouttes d'eau : on l’observe donc avec le soleil dans le dos. L’aspect coloré résulte de la différence de réfraction entre les rayons de différentes couleurs qui entrent dans la goutte. Sur la figure ci-dessous, on peut voir nettement un arc-en-ciel (arc primaire), accompagné d’un arc secondaire moins lumineux. On remarque également que la zone intérieure à l’arc principal est plus claire que la bande sombre entre les deux arcs.

Crédits Photo: Fiona Storey / www.public-domain-image.com

Pour comprendre cet ensemble de phénomènes, il est nécessaire d’étudier la déviation d’un rayon solaire par une goutte d’eau suite à une première réfraction en entrée, une réflexion (partielle!) à l’arrière de la goutte, et une deuxième réfraction en sortie, comme défini ci-dessous. Par définition, l’angle de déviation D est l’angle entre la direction du rayon lumineux après déviation et la direction qu’il aurait eu en l’absence de déviation, c’est à dire s’il n’y avait pas eu de goutte d’eau. Cet angle est donné par la somme des trois déviations élémentaires occasionnées par chaque interface, ce qui nous amène à la formule simple D=π+2i-4r.

La complexité de l’étude provient du fait que les angles i, r, et donc D, dépendent du paramètre d’impact x avec lequel le rayon solaire arrive sur la goutte. La courbe de déviation de D en fonction du paramètre d’impact est présentée ci-dessous, à gauche. En cours, nous avons étudié cette fonction « à la main » et montré qu’elle passe nécessairement par un minimum. Cela implique que des rayons incidents différents subissent tous des déviations différentes, mais qu’on observe une accumulation de rayons lumineux à l’angle de déviation minimal Dmin. Cette accumulation de lumière est appelée une caustique.

La compréhension de l'origine de cette accumulation de lumière repose sur une analyse de la quantité de lumière qui sort de la goutte dans une direction donnée. Au voisinage du minimum de déviation, la courbe de la déviation devient très « plate » car la tangente à la courbe est horizontale. Ainsi, de nombreuses valeurs du paramètre d’impact conduisent à une déviation très proche de la déviation minimale: un rayon lumineux pris au hasard a donc « plus de chances » d’être dévié avec un angle proche de Dmin que selon n’importe quel autre angle. Il y a au final beaucoup plus de lumière déviée avec un angle proche de Dmin que de lumière déviée dans les autres directions.

On peut remarquer également que les rayons issus d’un même « pinceau de lumière » (ensemble de rayons lumineux proches les uns des autres) seront en général séparés rapidement après déviation par la goutte. La luminosité du faisceau va donc fortement diminuer après déviation, puisque l’énergie lumineuse transportée sera de moins en moins concentrée au fur et à mesure que l'on s'éloigne de la goutte. Comme le montre la figure du centre ci-dessous, une exception à cette règle intervient lorsque le pinceau lumineux est dévié au minimum de déviation. Dans un tel cas, l’énergie lumineuse reste concentrée dans un pinceau de rayons parallèles, et l’intensité du faisceau reste intense même à très grande distance.

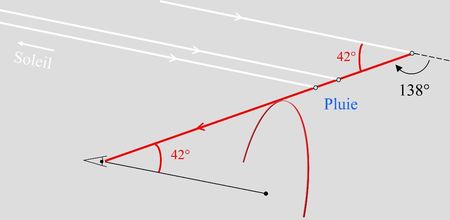
Nous avons étudié la variation dD induite par une variation dx du paramètre d’impact, et avons montré que dD/dx est égal à 0 pour une valeur de x bien précise (x/R=0.86 pour un indice de l’eau n=4/3). On en déduit aisément la valeur de l’angle de déviation minimale : Dmin=138°.  Bien sûr, il y a des rayons qui sont déviés d’un angle plus grand que 138° : c’est d’ailleurs ce qui explique la « zone claire » mentionnée précédemment. Mais si l’on s’intéresse à l’arc-en-ciel en lui-même, il n’est besoin que de connaître la valeur de Dmin : les gouttes qui participent à l’observation de l’arc-en-ciel par notre œil sont toutes celles qui ont dévié les rayons du soleil d’un angle égal à 138°.

Comme le montre la figure ci-dessous, et en prenant en compte l’invariance par rotation du problème autour de l'axe Soleil-oeil, on se rend compte que les gouttes satisfaisant à cette condition sont toutes celles qui sont situées sur un cône de 42° d’angle ayant pour sommet l’œil, et centré sur l’axe Soleil-œil. L’œil ne peut pas mesurer la distance à laquelle est placé une goutte qui l’éclaire : tout ce qu’il voit est un arc de cercle  lumineux de 42° de rayon apparent. Notons que s’il y avait des gouttes d’eau partout le cercle serait complet; sur Terre, on n’observe naturellement qu'un morceau supérieur de ce cercle puisque la partie inférieure est "dans le sol", où il n'y a pas de gouttes d'eau.

On comprend aisément le phénomène de séparation des couleurs, en rappelant que l’indice d’un milieu dépend de la couleur (la longueur d’onde) de la lumière utilisée. Cette dépendance de l’indice en fonction de la longueur d’onde est appelée la dispersion; la figure ci-dessous présente par exemple la courbe de dispersion de l’eau. A chaque couleur correspond un indice, donc un angle de déviation minimal, et donc un arc particulier : par exemple un arc de 41,5° pour le bleu et un arc de 43° pour le rouge. L’arc-en-ciel proprement dit résulte de la superposition des arcs issus de chaque longueur d’onde.

En s'intéressant aux rayons deux fois réfléchis à l'intérieur de la goutte, on explique également l'existence d'un arc en-ciel-secondaire, plus large et moins intense (puisqu’il fait intervenir deux réflexions partielles au lieu d’une seule) que l'arc principal. On peut également montrer que l'ordre des couleurs est inversé pour ce deuxième arc-en-ciel par rapport au premier.

Une version imprimable de ce résumé de cours peut être téléchargée en cliquant sur ce lien.

Comments

[raoul]

et si on ferme les yeux, est-ce que il y a diffraction, hein ?

[georges]

le calcul de l'angle du cône de l'Arc-en-ciel (variable selon la longueur d'onde, moyenne de 42°) est clair (ici ou ailleurs), mais qu'est-ce qui détermine la distance de l'arc en ciel?