Cours n°2 – Histoire de la physique de la lumière, première partie

Les tous premiers concepts de la physique de la lumière remontent à l’antiquité gréco-romaine :

• Les « verres ardents » qui permettent d’allumer un feu en concentrant les rayons du soleil.

• La légende - très certainement fausse - d’Archimède qui aurait réussi à incendier la flotte romaine à Syracuse grâce à des miroirs focalisants.

• Le conflit entre les atomistes (Démocrite) et les pythagoriciens (Euclide puis Ptolémée) sur la nature de la lumière : les premiers affirment que la lumière est constitué d’atomes qui s’échappent de la matière, les seconds pensent que l’œil envoie des rayons qui sondent l’espace alentour à la manière d’un radar.

• L’empereur romain Néron qui utilise une lame de verre colorée (soi-disant une émeraude) pour améliorer sa vision lors des combats de gladiateurs.

Il faut ensuite attendre presque un millénaire avant que des physiciens arabes posent les bases théoriques claires de la physique de la lumière. Ibn Sahl a ainsi été le premier à trouver la loi exacte de la réfraction en 984 – mais son manuscrit n’a été découvert et reconstitué qu’en 1993 par un historien des sciences… de l’Université Paris 7. A partir de 1040, les découvertes arabes seront heureusement (bien que partiellement) exportées grâce au traité d’optique du physicien Ibn Al Haytham, traité qui influença les scientifiques occidentaux pendant six siècles.

Ibn-Sahl, 940-1000

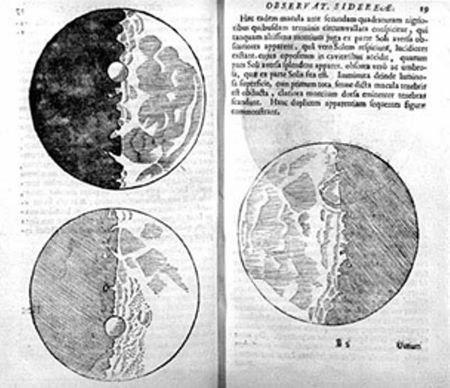
Suite à l’apparition des premières lunettes correctrices, au 13ème siècle à Florence, l’artisanat des lentilles se développe et permet à Galilée de réaliser en 1609 sa célèbre lunette. Galilée (1564-1642) est l’un des pères fondateurs de la science moderne: il montre que la découverte scientifique s’obtient en observant expérimentalement, activement, la nature. La vérité n’est pas nécessairement inscrite dans la bible, elle ne vient pas du haut mais elle est à nos pieds, l’homme doit se pencher pour aller la chercher. Sa lunette est l’objet emblématique de cette démarche et aussi objet mythique dans l’histoire de l’optique. Elle lui permet de découvrir une moisson de nouveautés astronomiques : lunes de Jupiter, « oreilles » de Saturne (qui deviendront plus tard les anneaux), relief lunaire, nouvelles étoiles, tâches solaires… L’année 2009 était, à l’occasion de ce 400ème anniversaire, l’année mondiale de l’astronomie.

Galileo Galilei, 1564-1642

Notons toutefois que Galilée ne cherchait pas à être un théoricien de l’optique; c’est à l’hollandais Johannes Kepler que nous devons la notion d’image et la compréhension des processus de la vision (1602), tandis que Snell en 1621 puis Descartes en 1637 retrouvent successivement (indépendamment?) la fameuse loi de la réfraction. En 1657, Fermat énonce le principe qui porte son nom (cf cours 1), en désaccord avec l’interprétation de Descartes : Fermat pense que la lumière se propage plus lentement dans le verre que dans l’air, tandis que Descartes justifie sa  loi en considérant que les « particules de lumière » sont accélérées lorsqu’elles pénètrent dans le verre.

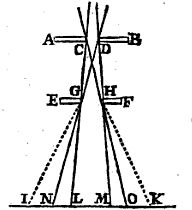
On se doute déjà à cette époque, en effet, que la vitesse de la lumière est finie, mais il faut attendre 1676 pour que le danois Römer en fasse la première démonstration. Il étudie les éclipses du satellite de Jupiter, Io, qui sont occasionnées à chaque fois que Io passe dans le cône d’ombre de Jupiter: ces éclipses constituent un processus parfaitement périodique dont la période est de 42h30, un peu comme une horloge extrêmement lente. Ce que Römer constate et parvient à comprendre, c’est que nous observons ces éclipses avec un certain décalage temporel, par rapport au moment où elles se produisent (décalage associé au temps non négligeable mis par la lumière pour parcourir la distance Io-Terre). Or, comme le montre la figure ci-dessous, le trajet Jupiter-Terre dépend de la position relative des deux planètes. L’horloge observée n’est donc pas parfaite: l’éclipse nous apparaît tantôt avec un peu de retard (lorsque le décalage temporel est plus long) et tantôt avec un peu d’avance (lorsque le décalage est plus court), en fonction des saisons. En mesurant ces décalages, et connaissant le rayon de l’orbite terrestre, Römer obtient la première mesure de la vitesse de la lumière : c=212 000 km/s. Il faudra attendre près de deux siècles avant qu’une mesure plus précise soit obtenue.

A peu près à la même époque, dans un ouvrage publié en 1665, Francesco Grimaldi démontre expérimentalement que la lumière est déviée au passage à travers un trou (figure ci-dessous), et que le faisceau lumineux transmis présente des alternances de couleurs au fur et à mesure qu'on s'éloigne de la zone centrale blanche. Grimaldi nomme ce phénomène diffraction et, pour l’interpréter, suggère que la lumière est un fluide en mouvement ondulatoire rapide. Dans les années suivantes, le conflit entre l’interprétation corpusculaire de la lumière (qui date des atomistes), et cette toute nouvelle interprétation ondulatoire, sera incarné par deux grands physiciens : Isaac Newton et Christiaan Huygens.

Francesco Maria Grimaldi, 1618-1663

Newton (1642-1727) est l’auteur d’avancées majeures autant en mécanique qu’en optique. Il doit avant tout sa renommée immense à sa théorie de la gravitation universelle, et aux lois fondamentales de la mécanique classique. L'image ci-dessous montre le cahier d'expériences de Newton dans lequel il reporte la décomposition de la lumière blanche par un prisme. Lorsque l'une des composantes (c'est à dire l'une des couleurs du spectre) est isolée par un trou et passe dans un second prisme, elle n'est pas à nouveau décomposée.

Isaac Newton, 1642-1727

Pour Newton, la lumière est constituée de petites particules qui voyagent des objets vers notre œil : il considère que la réflexion, la réfraction et la diffraction sont des déviations de la trajectoire des particules, déviations associés à des forces exercées par les matériaux. Il ne parvient toutefois que difficilement à répondre à une question fondamentale : comment se fait-il que certaines des particules soient transmises, alors que d’autres sont réfléchies ? Certaines particules seraient-elles soumises à une « force réfractive », tandis que les autres sont soumises à une « force réflexive » tout à fait différente?

Newton a également laissé son nom à un phénomène découvert par Robert Hooke en 1665 : les « anneaux de Newton ». Lorsqu’on plaque une lentille convexe sur une lame de verre, on obtient une mince couche d’air d’épaisseur variable entre la lentille et la lame. Si on éclaire ce système optique (lentille+air+lame) avec une lumière blanche, et si on regarde la lumière réfléchie ou transmise, on observe un système d’anneaux colorés, avec des couleurs similaires aux irisations des bulles de savons. Si on éclaire le système optique avec une lumière d’une seule couleur, on observe à la place un système d’anneaux alternativement sombres et lumineux. Ces anneaux prouvent que la quantité de lumière réfléchie par le système optique dépend de l’épaisseur de la mince couche d’air : en effet, cette épaisseur augmente au fur et à mesure qu’on s’éloigne du point de contact entre la lentille et la lame.

          

Isaac Newton, 1642-1727

Cette expérience est un cas typique de « non-localité » difficile à interpréter dans le cadre de l’interprétation corpusculaire. Tout se passe en effet comme si les particules de lumière, au moment d’arriver sur une interface (lame-air), étaient influencées par la position de l’autre interface (air-lentille), et que cette influence déterminait le choix final (ie, réflexion ou transmission). L’interprétation corpusculaire est ici soumise à rude épreuve, conduisant Newton à des hypothèses relativement confuses.

Pour Christiaan Huygens, au contraire, la lumière est un phénomène ondulatoire : tout comme le son est une vibration de l’air, la lumière est une vibration de l’« éther », un fluide infiniment subtil qui remplirait tout l’Univers et serait capable de s’insinuer dans tous les matériaux. Huygens décrit comment une vibration en un endroit conduit à faire vibrer l’éther alentour, qui conduit à faire vibrer l’éther un peu plus loin, et ainsi de suite. Il comprend que - si l’on regarde la résultante de toutes ces vibrations – les ondes émises par un point lumineux se propagent simplement en cercles concentriques

Christiaan Huygens (1629-1695)

Son résultat le plus marquant est la démonstration des lois de la réfraction et de la réflexion, partant de l’hypothèse que les ondes lumineuses sont ralenties à la traversée d’un matériau. Par contre, il ne parvient pas vraiment à expliquer le phénomène des ombres projetées par les objets, phénomène qui prouve que la lumière ne contourne pas les obstacles, contrairement aux ondes sonores. Newton utilise cet argument pour rejeter en bloc l’interprétation ondulatoire, et les théories ondulatoires et corpusculaires vont s'affronter pendant plus de deux siècles, aucune des deux ne semblant décrire de manière satisfaisante l'ensemble des phénomènes lumineux.

Un deuxième grand succès de Huygens a été l’étude du phénomène de biréfringence en 1678. La biréfringence est la propriété que possèdent certains cristaux de séparer un rayon lumineux en deux lors de la réfraction sur leur surface: l’un des rayons vérifie la loi de la réfraction (rayon « ordinaire »), tandis que le deuxième suit une loi beaucoup plus complexe (rayon « extraordinaire »). Comme le montre la photographie ci-dessous, l’image d’un objet placé derrière le cristal se trouve dédoublée. Huygens explique cette double réfraction par sa théorie ondulatoire: le rayon ordinaire correspondrait à une onde se propageant dans l’éther, tandis que le rayon extraordinaire correspondrait à une onde se propageant de proche en proche dans les particules du cristal. Son analyse extrêmement précise lui permet de démontrer une formulation exacte de la loi du rayon extraordinaire, à partir de sa théorie ondulatoire, en supposant que les ondes lumineuses dans le cristal se propagent plus vite dans une direction que dans l’autre (propagation anisotrope).

Newton traite toutefois cette découverte avec désinvolture, et même avec une dose de malhonnêteté. Il rejette la démonstration d’Huygens sans même l’examiner, et propose en 1704 sa propre formulation de la loi du rayon extraordinaire, formulation qu’il ne cherche d’ailleurs pas à justifier. Ses deux principaux contradicteurs étant alors morts (Huygens en 1695 et Hooke en 1703), il faudra attendre une centaine d’années avant que des physiciens ne prennent la peine de refaire l’expérience et de vérifier les calculs, constatant ainsi que la formule de Newton était fausse. Cet épisode illustre à la fois l’influence écrasante de Newton, et le fait que la révolution galiléenne ne s’était pas encore définitivement imposée: de nombreux scientifiques du 18ème siècle considèrent encore que la vérité se trouve dans les textes prestigieux des anciens.

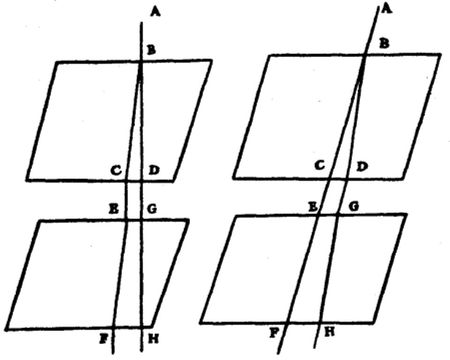
A son crédit, il faut toutefois remarquer que Newton avait commencé à interpréter un aspect important du phénomène de biréfringence. Huygens avait en effet noté, sans parvenir à l’expliquer, que lorsque les rayons ordinaire et extraordinaire ont été séparés par un premier cristal, ils ne sont pas dédoublés à l’arrivée sur un second cristal identique (voir ci-dessous). L’interprétation de Newton est que les rayons lumineux ont une « forme » qui les conduit à avoir deux comportements possibles (réfraction ordinaire ou extraordinaire) suivant leur orientation par rapport au cristal. Il est alors normal que les rayons ayant présenté un comportement ordinaire dans un cristal fassent de même lors de la traversée d’un second cristal identique, puisqu’ils ont conservé leur orientation.

Christiaan Huygens (1629-1695)

Etienne Louis Malus, en 1808, renforce cette idée en introduisant la notion de polarisation de la lumière : il considère que les « molécules lumineuses » ont des pôles (c'est-à-dire une orientation propre). Il imagine qu’au moment de traverser une surface, les molécules sont forcées de se polariser (c'est-à-dire de s’orienter, soit perpendiculairement, soit parallèlement au plan d’incidence). Dans le cas des cristaux biréfringents, Malus introduit des « forces réfractives » différentes pour les deux polarisations possibles, donnant lieu aux deux réfractions. Il parvient à retrouver les lois d’Huygens, explique tous les phénomènes associés aux expériences à plusieurs cristaux, et étudie également la polarisation de la lumière lors de sa réflexion sur une surface. Cette analyse très complète est perçue par de nombreux physiciens comme une confirmation claire de la théorie corpusculaire.

Une version imprimable de ce résumé de cours est disponible en cliquant sur ce lien.

Comments

[llanco]

Bonjour,

C'est une belle idée de projet. Ecrivez-moi à l'adresse loic(dot)lanco(at)lpn(dot)cnrs(dot)fr, afin que je vous mette en contact avec le responsable des TP d'optique en L3.

Loïc Lanco

[Julien Porceddu]

Bonjour,

Dans le cadre du Projet de Physique du Semestre 2, j'ai choisi pour projet la Polarisation de la Lumière.
Lors d'un de vos cours du 1er Semestre, vous avez parler d'une expérience mettant en évidence les propriétés caractéristique de la Polarisation de la Lumière avec le Cristal de biréfringence, j'aimerais donc savoir où il était possible de s'en procurer un, afin de reproduire et comprendre par moi même cette expérience.

Je vous remercie pour votre attention, Cordialement J. Porceddu.